RECURSIVE PROBLEM OF CALIBRATION
OF EXPERT SYSTEMS
Department of Computer Science
500 Glenridge Ave.
ST.CATHARINES, ONTARIO
CANADA L2S 3A1
January 1998
ABSTRACT
A model of modeling processes is presented here, including the analysis of the ways of creating systems that use their own experience of past executions of algorithms in order to improve performance. The methods of algorithmic treatment of the mechanisms of evolution, intuition, consciousness and learning are suggested. The ability to best forecast its own sensory stimuli is identified as the winning evolutionary criterion for calibration of expert systems. Fundamental mechanisms for detecting available parallelism in algorithms and methods of search for and classification of optimal processor configurations are described.
NOTE: The mathematical notation presented is best viewed using Internet Explorer 4.01 or later.
LEARNING AND PERFORMANCE IN EVOLUTIONARY CONTEXT
The issue of measurement of expertise attracts much attention within and outside the Artificial Intelligence (AI) community. Similarly, there is much discussion on the concept of expertise, knowledge, etc., with stress frequently put on these supposed features of the natural expert systems (humans, other animals, etc.) that artificial expert systems (computers, etc.) cannot possibly have. For some recent affirmations of these positions please peruse [Searle, 1980], [Penrose, 1989], [Rychlak, 1991], while one of refutations of such a stance is the work of [Hayes, Ford, Adams-Webber, 1992].
The AI community is typically more preoccupied with pushing the limits of the technologically possible rather than with this discussion. This is regrettable, because some points of essential importance are being raised here, which have fundamental relevance to future technological developments.
One of such fundamental concepts frequently avoided by the computer scientists in general and the AI community in particular is the concept of evolution. It is usually deemed too general to be of practical use, or, some would even say, tautological ('survivors survive'). Only with reluctance will computer scientists agree that evolution is what they frequently term recursion. Suggestions that evolutionary strategies may be the most effective means to create complex expert systems are frequently met with raised eyebrows. Attempts to justify these suggestions by pointing out that the most complex expert systems known to date were created through an evolutionary (i.e. recursive) process are usually not found to be particularly convincing. Even the fact that non-trivial programs can only be developed via a number of stepwise refinements, is not generally considered to be of evolutionary significance. Similarly, the design and creation of ever more complex computers (or any products, for that matter) comes about only through a process of stepwise refinements... We simply participate in the evolutionary process, whether we like to acknowledge it or not.
In the light of the above, the author decided to join the debate with the intent to offer a certain point of view on the nature, structure and performance of the expert systems, both 'natural' and 'artificial.' Indeed, in view of the lack of precise scientific distinction between things 'natural' and 'artificial', the reasoning offered here does not rely on such classification. At the same time, the author's intent is to be as practical as possible, rather than philosophical. The author will therefore suggest a particular systems development methodology that would allow us to build ever more sophisticated expert systems. The most sophisticated systems we know are capable of programming themselves.
Before we start the reasoning, a word of excuse: The reasoning that follows stems from the underlying assumption that any expert system of sufficient complexity, left in an unfamiliar environment, will be able to learn and adapt to that environment, given sufficient time. One could say that such a system could develop its own 'science'. Consequently, in an attempt to explain how this could happen the author cannot help making some comments on the fragility of the established foundations of several scientific disciplines, including the author's own. This fragility is also our great modeling opportunity.
ON THE FRAGILITY OF SCIENCE
To establish a common starting point in the proposed way of reasoning, let us consider the universally familiar concept of energy.
The Encyclopedia of Physics [Lerner, Trigg, 1991] defines energy as:
"... a certain abstract quantity that an object (either matter or wave) is said to possess. It is not something that is directly observable, although in certain cases the behavior of the object possessing a particular amount of energy can be observed and the energy inferred."
Obviously energy is a fiction, a symbolic quantity that we associate with objects in order to predict their behavior. The general feeling we share that this concept must be 'true' stems merely from its repeated successful application in our forecasting endeavors. Before we struck on the concept of energy, other symbolic quantities were utilized in our forecasting, although less successfully. Should we discover some particular symbolic quantity allowing us to better forecast object behavior (i.e. faster, or more accurately, or preferably both) we would term that new quantity 'true' and abandon the use of energy. Physics has abandoned many obsolete concepts like luminiferous ether, phlogiston, etc.
In similar vein we could identify as fiction all basic concepts that 'hard' sciences use. One such fundamental concept is time. The Encyclopedia of Physics does not even give its definition, but merely describes some properties of this nebulous entity. Significantly, physicists do not agree between themselves whether time is an objective entity, or merely our construct (symbol) that we use in our description of the world. In this paper the author argues that time is a symbol manipulated by the expert systems.
One thing is pretty certain: without the concept of time the 'hard' sciences that are in business of describing reality, collapse. We have picked examples from physics, generally deemed the 'hardest' of all sciences, but other sciences fare no better: biology, being the origin of the idea of evolution, fundamental to this paper, is in business of describing the properties of life without being able to define what life is [Langton, 1989].
This is not a criticism of the scientific method, nor of the particular sciences mentioned. It is intended as an illustration of the concept of reality being a fictitious symbol that we use to describe the environment we inhabit. The scientific method, with all its imperfections, is the best tool we have to study the environment. It permits us to perform experiments to verify our models of the environment, and reject those found to be false. Without the ability to perform experiments we are left at best in the domain of philosophy. Conflicting philosophical theories cannot be reconciled by experimental verification.
If even the concepts of 'hard' sciences are figments of our imagination, is there anything we know of, that exists objectively? Fortunately, the answer to that question is affirmative. 'Real' are our own sensory stimuli. We can only speculate about their meaning, interrelationships and causes. Such speculation, when pruned by experimentation, is called science. In this paper the author argues that the essence of life is the competition for survival among expert systems. The environment as winners in this competition selects systems capable of forecasting their future sensory stimuli with longer range and superior accuracy, using their current and past stimuli as data.
At this point it might be useful to describe the biological concept of evolution, from the point of view of computer science.
EVOLUTION IN COMPUTING TERMS
In order to prolong its own existence, any system equipped with sensors and effectors (actuators) faces two fundamental Boolean decisions.
The first of them is whether to react or not to react to its current sensory stimuli. Our observation shows that the environment tends to favor some systems that choose to respond to their current stimuli. These systems are rewarded in the sense that their probability of survival is increased. We say that their reactions are 'correct' or 'true'.
In principle, systems reacting to their stimuli may fare worse than these systems that do not react at all. We term such suicidal reactions 'false', ‘wrong’, ‘bad’. The environment tends to penalize such systems by terminating their existence. The systems that respond to their current stimuli could be termed combinatorial automata. The environment seems to select some of them.
When eliminating ill-adapted systems (i.e. systems frequently producing 'wrong' reactions) the environment acts selectively: systems exhibiting such behavior more frequently have a higher probability of being eliminated. Luckily, not all mistakes are lethal: systems allowed to survive their mistakes are thus given the opportunity to correct their future behavior. We say that systems taking this opportunity are capable of learning.
There is a lot of mysticism associated with learning. The most extreme is the view that the act of learning defies algorithmic treatment. In the latter section of this paper we will contradict this view by formulating the universal algorithm for learning.
We have also observed that sometimes even the knowledge of the correct response to current stimulus does not guarantee the survival of an expert system. There may be not enough time to execute the response action. Early expert systems have discovered that future sensory stimuli can be forecast more or less reliably using the current and past stimuli as data. Some systems utilizing this strategy are capable of further enhancing their chances of survival: with 'correct' forecasts they gain more time to act on the stimuli.
The second fundamental Boolean decision every system faces is whether to start forecasting activity. These that do may be called sequential automata.
From the evolutionary standpoint, thought is nothing more than forecasting activity, i.e. an exercise in guessing the future. This activity is not without danger: while correct guesses may enhance chances of survival, wrong guesses may have consequences worse than no guesses at all. The systems capable of thought are expert systems. The expertise of some is better than of others.
Given two experts capable of forecasting an equally distant future, the one producing forecasts of statistically better accuracy is considered superior. Similarly, given two experts producing forecasts of the same accuracy, the one capable of forecasting a more distant future is considered superior.
For a single expert system, the odds against adopting a successful forecasting strategy are tremendous. Every expert system faces an extremely large (but finite; details follow) number of forecasting strategies to consider, in order to identify the optimal one. Additionally, adoption of a wrong strategy may lead to the destruction of the expert system.
Luckily, we inhabit an environment that appears to subtly favor thoughtful behavior. In this environment it is easier to build large numbers of simple expert systems (i.e. with fewer sensors, effectors, and computational elements) than of complex ones. Simple systems have fewer strategies to ponder. This number of strategies may be further reduced if the forecasting horizon is limited. With vast numbers of expert systems present in various niches of the environment, even if forecasting strategies are selected uniformly at random, some systems will survive longer than others. Their mere existence identifies forecasting strategies suitable for their environmental niches. The interactions of surviving systems may lead to the creation of more complex offspring. For details of such reproductive interactions, seen from the computing perspective, please peruse any book on genetic programming, for example [Koza, 1992]. The main focus of his paper will be on the act of automatic learning.
In order to improve their forecasting performance, expert systems should be able to learn on their own. To be able to learn, an expert system must be equipped with some processing power and memory.
MEASUREMENT OF EXPERTISE
In our scientific endeavors we (humans) aim at the creation of models of the environment that would enhance our chances of survival. We surround ourselves with fictitious symbols that we manipulate in our forecasting endeavors. Arguably, mathematics is nothing more than a collection of useful symbols and rules of their manipulation. As long as these symbols serve us well, we tend to forget that we are the creators of these symbols and start to believe that these symbols are the objects, or attributes of the objects we observe.
Sometimes we continue to manipulate symbols that we already know that are 'false.' For example, in everyday life we use Newtonian rather than relativistic models in predicting object behavior. The falsity of these models does not bother us exceedingly, as long as these models are useful in our forecasting activities, i.e. permit us to arrive at certain forecasts of desired accuracy within certain time limits. Temperature, being a mere numerical generalization of our own sensory perception of hotness or coldness, is one such symbol: it must be patently 'false' since it has no meaning at the level of elementary particles. Strictly speaking, it has therefore no meaning with regard to any object made of elementary particles.
Knowledge is another such abstract symbol, i.e. a fictitious quantity, which we attribute to some subsets of nature (expert systems). We do not observe knowledge directly; we merely observe the behavior of systems that we suspect to be 'knowledgeable'. Using our observations we try to evaluate the 'amount' of knowledge the system might have.
Every forecast has a deadline after which it is useless. To illustrate this, let us suppose that a certain person, calling herself /himself an expert claims that s/he has the ability of forecasting with superior accuracy the weather for tomorrow, using the data of today. Making such a claim is not sufficient to be recognized as expert. Indeed, should the person submit that his/her skill is subject to a handicap that it takes him/her two days to compute the forecast for tomorrow, we would regard the whole claim with certain skepticism.
The necessity of being able to meet certain deadlines is essential here. For 'artificial' expert systems it translates into the need to have sufficient computing power. As to our human 'expert candidate', his/her forecasting feats must be carefully observed, and the success to failure ratio of the forecast must exceed certain threshold in order for us to grant him/her the expert status. With the ratio below the threshold value we are likely to reject the hypothesis that the person is an expert, and attribute his/her sporadic forecasting successes to mere luck.
Indeed, we could propose here a numeric tool for measurement of systems' expertise. The quality Q of a given forecast could be expressed as:
Q = (td - tf)/e
where e is the non-negative (absolute, square, etc.) value of the error of the forecast, td is the time limit (deadline) imposed by us on the expert system, and tf is the time needed by the system to produce a forecast. Consequently, the quality of a forecast is proportional to its accuracy and to the amount of time left to act on a forecast.
In the same vein we could come up with a numerical tool permitting us to distinguish between expert systems and those that are just lucky. For example we could decide to regard as experts only these systems that consistently give forecasts of quality exceeding some arbitrary threshold value. (Obviously, systems with a negative forecast quality, i.e. not meeting the deadlines, need not apply). This tool, when used in a controlled environment, could be utilized to calibrate expert systems.
Currently, knowledge is acquired by expert systems in two ways. A direct way is through observation of arbitrary objects of nature, while the indirect way is to observe the behavior of other expert systems. The indirect way is available only to expert systems of some complexity: they must be able to recognize another expert system when they encounter one.
THE LEARNING ALGORITHM
Having discounted all concepts used by hard sciences as fiction, it would appear that the author has painted himself into a corner. How to proceed with the scientific reasoning in this paper? There is no choice but to use some fundamental scientific concepts. How could their use be justified?
Yes, these concepts are a fiction, but the fiction describing the environment best to date. The author claims that the reasoning presented in this paper is 'true', because the presented ideas permit us to create new expert systems with performance superior to present expert systems. We participate volens nolens in the evolutionary process. This process resembles the act of climbing a structure with a moveable ladder: having climbed to some level and having moved the ladder to span the next level, it may appear unbelievable to find ourselves at the current level.
Consequently, it may happen that in the future new paradigms for creation of ever more sophisticated expert systems might emerge. Each of these paradigms would be deemed 'true' at the appropriate stage of the evolutionary development. This paper focuses on the paradigm that is currently 'true'.
To play it safe, only two concepts of physics will be used: these of an atom and of energy. The version of the fundamental learning algorithm that is about to emerge will be impractical, but conceptually robust. We will postpone a bit the considerations of practical refinements.
Consider an arbitrary expert system. All expert systems we know are made of a finite number of elements (atoms). (Certain groupings of atoms of the most complex systems we know were named cells by the biologists). Consequently, every expert system contains a finite number of sensory elements. The energy absorbed by or returned to the environment changes the state of each sensory element. As the physicists teach us, energy comes in quantified amounts, the number of states of each sensory element must be finite. (Strictly speaking, the quantification alone guarantees only that the number of these states be countable. This number must be finite, though: energy levels above certain threshold lead to the destruction of the sensory cell, not to mention the expert system).
Given an expert system containing C sensory cells, each of the cells being in one of at most N states, the entire system is capable of recording up to NC of different sensory states. It is therefore possible to uniquely number these states. From now on, when talking about the sensory stimuli of an expert system, we will refer to these numbers.
Let S be the collection of all possible stimuli for a given expert system. Throughout its life span the system observes a series {si} of sensory stimuli, each stimulus si � S. If the system were to remember all of its stimuli, they could be stored in a linked list. Such linked list could be considered time, relative to that expert system. For the mathematicians, we could even define:
Time: a relation T between two stimuli sa and sb. We write sa T sb iff a < b.
In plain language, we say that sa precedes sb, or that sb follows sa.
Using this approach, we can reduce the learning behavior to one problem: Given a finite series of numbers {si}, guess the next number. In life, expert systems capable of more reliable guesswork survive longer.
From the strict mathematical standpoint, such guesswork constitutes an ill-posed problem. To illustrate that, consider for example a sequence 0, 2, 4, 6, 8. What is the next number? Most readers will probably guess 10, noticing that the series consists of several consecutive even numbers. The forecasting formula in this case would be ai = 2*i, for i = 0, 1, 2, ... permitting us to guess any number in this sequence.
However, if we extend the sample sequence to read 0, 2, 4, 6, 8, 0, 2, 4, 6, and ask again to guess the next number, an observant reader might answer 8, assuming that we started repeating the original sequence again. The forecasting formula in this case could be ai = (2*i) mod 10, for i = 0, 1, 2, ...
As every mathematician will tell us, there are an infinite number of formulae that produce identical finite subsequences. Why do we then select particular formulae, and what is the selection criterion? The author would argue here that the criterion is the computational complexity. We prefer formulae that contain all information afforded by the sample and permit us to come up with forecasts as fast as possible.
There is a number of commercial software products available, that are capable of guessing formulae to fit experimental data. It is tempting to build on this approach, perhaps by constructing parallel computers that would try a number of guesswork conjectures simultaneously. Instead of surrendering to that temptation, let us simplify the guesswork problem even further.
Bits can represent numbers. Instead of guessing the next number, given the finite sequence {si}, let us encode all the numbers in binary and consider an equivalent, finite binary sequence. The problem reduces to guessing the next bit. In other words, we have reduced intelligent behavior to a particular Turing machine, capable of reading and advancing tape in one direction only. This machine would be able to advance only if it guessed correctly the current bit. An ideal machine would never halt.
A plethora of digital design tools and methods now becomes available. One possible strategy would be to assume that the next bit is a Boolean function of the last bit, then of the last two, three, four, etc. bits. Every time a machine surviving the mishap of a wrong guess could take it as a hint of a learning opportunity. Its 'correct' reaction would be to increase by one the number of past bits considered in forecasting the future bit. Automatic methods exist to implement such Boolean functions as digital machines. The forecasting performance of such generations of machines would continue to improve. Such machines would be able to learn, i.e. to program themselves.
The presented reasoning is intended to illustrate our ability in principle to implement intelligent behavior in a machine. However, a straightforward adoption of this approach would be grossly inefficient. If we aim at the creation of expert systems that efficiently acquire knowledge, we must first understand the principles of human knowledge acquisition. How then do humans reach the situation of understanding a typical object? We collect the information about the object via the observables, i.e. sensory stimuli. We have no choice but to assume that the values of these stimuli are in some correlation with the attributes of the object itself. The relationship between the observables constituting the situation of understanding is depicted in the Fig.1. as follows:
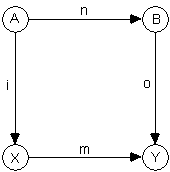
Fig.1. Standard graph depicting the situation of understanding a typical natural object n, in terms of its model m, and the model inputs i and outputs o.
Having observed some natural object, we try to divide the observables into two groups, called inputs and outputs and try to forecast the values of outputs in terms of the values of inputs.
Let us pick a familiar object to illustrate the above diagram: a car. A car is a system with some observables which we divide into inputs (gasoline, etc.) and outputs (exhaust fumes, etc.). To say that we understand how a car works means that we arrived at the conceptual model of a car. Such a model processes some logical equivalents of car inputs to forecast the logical equivalents of car outputs. (Obviously, the model of a car that we carry in our heads does not consume gasoline nor produce fumes!).
In general, we have an understanding of the natural object in terms of its inputs A and outputs B, if we can construct its model in terms of logical input equivalents X and output equivalents Y so that for every value a � A we end up with the same value y � Y regardless which set of arrows we follow in Fig.1. Mathematicians would say that the graph in Fig.1. commutes, i.e. given we treat n, i, o, m as functions operating from/to the sets A, B, X, Y, we achieve the condition of commutativity:
" a � A: m(i(a)) = n(o(a))
with the additional requirement that the left side of the above equation of commutativity is evaluated faster than the right side of it and the assumption that we perform the calculations with infinite accuracy. This is an idealization of a real life situation, of course. Typically we arrive at two different values y1 = m(i(a)) and y2 = n(o(a)) and as long as y1 is 'close' to y2 we prefer to assume that our model is correct but the observations and calculations are subject to inevitable errors (rounding errors in observation, computation, etc.). Otherwise we assume that our model is wrong. Statistical tests help us here.
A subtle point of fundamental evolutionary significance must be raised here. What if we perform an experiment in which we find y1 = y2? Does this imply that our model is correct? Not necessarily: the correctness of the model is verified only if we obtain y1 = y2 for all a � A. It is typically impractical to verify validity of the model by scanning all possible values of a. Most of the time we have to content ourselves with models that are partially correct, i.e. we know that they produce the condition y1 = y2 for some tested values of a � A only. Additionally, our sensory and computational apparata are subject to unavoidable errors (rounding, etc.). The simpler the expert system (in terms of the number and type of its sensory and computational elements), the larger and more likely such errors.
Matters get more complicated when we consider real expert systems. Such systems perform calculations with finite precision. It is therefore conceivable that an expert system might be fooled by its own hardware into believing that y1 = y2 when these values are different but sufficiently close. The simpler the expert system is (in terms of the number of its sensory and computational elements), the easier it can be fooled this way. Fooled systems are more likely to be destroyed by the environment. Luckily, the environment compensates for that: as said before, it is easier to create large number of simple systems than of complex ones. The larger the number of systems, the higher the probability that some of them will not be subjected to such tricky conditions. The systems spared such experiences have better chances of survival and producing offspring.
Humans do not like to be fooled in this way. This is why we took to using telescopes, microscopes, and other tools improving the precision of sensory perception. Of course these tools do not eliminate the problem completely; they only reduce the probability of being fooled by improving the accuracy of observation.
Fortunately, being wrong (i.e. considering two different values y1, y2, but y1 sufficiently 'close' to y2 to make them undistinguishable) is not always lethal, as indicated before. The higher the accuracy of perception and computation, the lower the chance of such conditions being fatal. Overall, the larger the pool of systems, the higher the chances that some will survive to produce offspring.
Incidentally, the diagram of Fig.1. applies to many specialized branches of AI research. Let us mention only the much-researched problems of image understanding and musical perception.
What is image understanding? It is a special form of image compression, allowing us to recognize and manipulate the components of an image by accessing and modifying the compressed version of the image.
Consequently, any machine having to decompress an image first in order to be able to manipulate its components cannot claim any understanding of it.
What about musical perception? Let us only hint that our feeling of musical pleasure has something to do with our ability to forecast the future musical passages with desired accuracy.
THE ISSUE OF INTUITION
One question was left unanswered: How do we know which observables are inputs, and which are outputs? In general, we do not usually have any a priori such knowledge; in principle we have to try all allocations. This looks like a very tedious task, and indeed, it is; but for every finite set of observables there is a finite number of such groupings to try. Biological systems tend to work on this problem in parallel: the bigger the number of researchers the sooner some of them will stumble upon the solution.
To simplify this tremendous job we tend to attempt to understand simpler objects first, i.e. objects with behavior describable with fewer observables. Fewer observables require consideration of fewer tentative groupings into inputs and outputs. To facilitate this task even further, humans frequently use high-speed computers. Indeed, with the advent of parallel computers many such groupings can be tried in parallel. Some AI researchers (including this author) would argue that brains are merely parallel computers, frequently used to attempt to try out many such groupings: this exercise would stop once a proper grouping is found. Could we then call the act of execution of such a program intuition if the program would suppress the results of computations until a suitable grouping was identified?
Usually we are satisfied, having found one set of inputs and outputs. Sometimes we are lucky and find more such sets. For example, electronic circuits are describable using at least two modeling paradigms: one that the application of voltages 'causes' the electric currents to emerge, the other being that the application of currents 'causes' voltages to emerge. (These are just two interpretations of the Ohm's law). This makes us realize that the whole concept of 'causality' is questionable. For deeper analysis of this subject please refer to [Wojcik, 1991].
THE ISSUE OF CONSCIOUSNESS
Our current office automation equipment frequently includes scanners. These devices are used for reading images and storing them in a raster form, perhaps to be pasted in the proper sections of relevant documents. The problem with this technology is that vast amounts of memory (disk and RAM) are needed to store raster data. This storage capacity problem is probably most acute in the area of medical imaging.
It would be much more efficient to store scanned data in a vector form. That is, instead of storing the information on a dot-by-dot basis, it would be preferable to recognize the images of known objects and store the information about these objects. For example, in an office automation workplace, a line segment could be stored by remembering the position of two end points, instead of positions of all raster points making up the segment. Such spectacular data compression allows also for easier subsequent image manipulation and editing.
Unfortunately, the implementers of this idea face great but temporary technological difficulties. The equipment capable of reliable vectorization of raster images should be capable of image understanding. While this topic is too specialized to be covered in detail in this paper, let us highlight the main technical difficulties. Consider the diagrams on the Fig.2.:
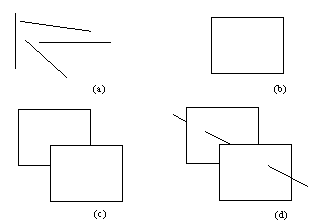
Fig.2. Vectorization and data compression performed automatically by our brains:
(a) This raster image is recognized to be made of four line segments. Such recognition offers spectacular data compression;
(b) Four line segments oriented like this are identified to be a rectangle. Further data compression becomes possible: instead of remembering the positions of four end points, we can remember only two corners and the fact that we have recognized a rectangle;
(c) Addition of four more line segments oriented like this makes us see (rightly or wrongly) two rectangles, resulting in further compression;
(d) Three more new line segments are interpreted as one (partially visible) line segment, but the whole picture becomes now three-dimensional. Each time we strive for maximal data compression.
Depending on the orientation of the line segments presented there, we form hypotheses what these segments represent. Assuming that our hypotheses are correct, we store the attributes of the objects the line segments are meant to represent, rather than the attributes of the very line segments. This allows us to obtain maximal data compression.
There is one problem with this activity: on what basis do we assume that we have guessed correctly that the segments really represent the objects we have tentatively identified? For example, the rear rectangle in Fig.2c. may not be a rectangle at all. We stand on very shaky grounds indeed. We proceed in this fashion only because of our training, making our guesswork correct most of the time.
Indeed, a scanner, or any other expert system equipped with raster vision (retinas, composite eyes, CCDs, etc.) must be given a chance of training itself, in order to statistically maximize its image understanding skills. We will discuss the practicality of this issue in some detail later in this paper. At this time we must only realize that raster vision does not allow us to recognize any object with certainty. Statistical pattern recognition is the only feasible tool. Usage of this tool, however, amounts to statistical hypothesis testing: such activity does not affirm any hypothesis with absolute certainty.
Instead of entering into lengthy statistical reasoning, let us make one fundamental example of this limitation. The simplest vector object (apart from the point) is a line segment. Any system with raster vision of finite resolution will not be able to distinguish between a straight-line segment and a short arc of a circle of sufficiently long radius. Both objects may produce identical raster images.
We might want to build an intelligent, 'sighted computer' inhabiting a two-dimensional environment of paperwork or film. It will continuously scan raster images trying to recognize objects and their interrelationships. It will 'think' of the objects as inhabiting a (possibly continuous) two-dimensional space. It will never know for sure that it has recognized a familiar object; it will merely run a certain statistical test and, should the test results exceed a certain level of significance (i.e. threshold of confidence), it will assume that the object is what it "thinks" it is.
Humans use this principle successfully when catching fish on artificial lures. The fish cannot tell the difference between lures and real prey. In this game a meticulous lure presentation is of paramount importance.
This may be so, but what does it have to do with consciousness? Well, imagine an autonomous, mobile and sighted robot inhabiting a three-dimensional environment and observing it by processing two-dimensional raster images. It will similarly continue to scan the environment in order to recognize the objects and their interrelationships. It will find it parsimonious (in terms of the amount of detail to be remembered) to 'think' of the objects as inhabiting a three-dimensional, possibly continuous space. It will continue to place these objects in that space.
Indeed, the whole concept of space appears to be our invention, much like that of time. We perceive the space we inhabit to be three-dimensional, not because it is objectively so, but merely because we need at least one extra dimension to understand various transformations of raster images formed on our two-dimensional sensory surfaces (skin, retinas, etc.). As we continue to observe our environment we need to introduce more and more dimensions to our concept of space, in order to be able to understand what we see. Interested readers with strong background in physics may wish to peruse the string theory, for example.
On the other hand, it might be worthy of note that some people blind since birth do not develop the concept of a 3D space. Their partners of conversation seem to appear from nowhere and to dissolve into nowhere, perhaps to reappear again.
If a given robot has an understanding of a 3D space, it will always 'see' one particular object in that space. Let us call this object self. Instead of remembering the relationships between every pair of identified objects, the robot will find out that it is simpler to express these relationships in terms of a reduced set of relationships to remember: these between every object and self.
This is what consciousness is all about. It is not a thing. It is a process of continuous updating the database of relationships between the identified components of the environment and self. Computer science defines a process as an act of execution of a computer program.
THE BREAKDOWN OF UNDERSTANDING
The situation of understanding, as described in Fig.1. is based on the assumption that there exists some functional relationship n between the inputs a � A and the outputs b � B of the observed object. Such a relationship is due to the interaction of parts of a natural object.
What if there is no such relationship? For example, truly elementary particles are not made of 'parts', therefore are not describable in terms of such relationship. In that case the diagram of Fig.1. degenerates to the one of Fig.3.
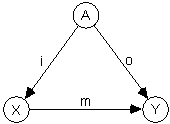
Fig.3. Degenerate graph depicting the situation of lack of understanding of a special object (elementary particle, etc.). It is possible to construct an infinite number of models m describing the special object in terms of model inputs i and model outputs o.
In such a situation we can construct an infinite number of models of such singular objects, i.e. an infinite number of function triplets {i, o, m} such that:
"a � A: m(i(a)) = o(a)
This is so because out of the functions i, o, m, n from Fig.1. only the last one operates independently of the observer. Lacking such down-to-earth reference, any observer is free to see what s/he wants to see. Those of us (humans) who had difficulty understanding the dual nature of elementary particles (matter and wave) know this feeling. In terms of 'artificial' expert systems we are free to build any hardware we deem fit to implement functions i, o, m.
DREAMS, EVOLUTION AND PARALLEL PROCESSING
The increasing need for more powerful computers is clear. Also obvious are the impressive developments in computing technology. If we were to attribute these developments to a single motivating factor, it could arguably be our ever-growing need for computational speed.
The R&D efforts aimed at the development of uniprocessors are well established, focused, and, so far, regularly productive, in terms of offering technically sound and financially feasible solutions.
A similar statement with regard to the development of multiprocessors cannot be made with equal confidence. The technological limits of the uniprocessor technology, dictated by the laws of physics (speed of light, noise levels, etc.), are universally recognized, thus offering the incentive to get us interested in parallel processing. Sadly, the implications of the conceptual limits, imposed by logic, tend to dampen our enthusiasm.
The halting program theorem is arguably the most important conceptual limit. It states that it is impossible to construct an algorithm capable of determining whether an arbitrary program, operating on arbitrary data, would halt or not [Boolos, 1987], [Davis, Weyuker, 1983], [Epstein, Carnielli, 1989]. Consequently, it is therefore impossible to write a program that would estimate the execution times of other programs, operating on given data, without actually executing these programs. After all, the undecidable question of whether an arbitrary (sub)program halts or not is a special case of a more general question: For how long does it run?
This dashes our hopes that application of parallel processing will prove to be a simple solution to our quest for ever greater computational speed. After all, our initial motivating impulse frequently was to allocate the subprograms of a given application program to various processors, with hope that the resulting configuration would execute successfully and faster than on a uniprocessor.
The widely recognized difficulty with this approach is that there are many ways of partitioning a program into subprograms. Then, for each such partition, there are many ways to allocate processors to the subprograms. Some of these allocations will be better than others in terms of execution speed. Some of them might perform worse than the simple execution of the entire program on a uniprocessor. Some even could result in an infinite extension of execution time, if a process were to be allocated a totally unsuitable processor.
How then are we to perform this search for optimal processor allocation? Manual search is out of the question. The search cannot be easily automated using some smart compiler technology that would somehow produce optimally allocated executable codes: compilers do not execute the programs, but only transform them into other programs that are equivalent from some point of view. Therefore, compilers cannot compare execution times of various allocations.
Is then such a search feasible and practical? Not to those sporadic users who want to run an application program only once for a given set of input data, obtain the result, and then return to their main activity. As to the feasibility: it will be evident a bit later that given the current state of computing technology a brute force search for optimal processor allocation for most commercial algorithms would take longer than the age of the Universe. However, for a user who routinely executes the same program with a given set of input data, it might be an interesting idea to own a program that would use its own execution experiences to keep configuring the computer on which it runs and reallocating processors to itself to run faster and faster.
Keeping all these difficulties and promises in mind, we still do a lot of research on parallel computing, the preferred architectures being processor pipelines, meshes of trees, hypercubes, symmetric multiprocessors, etc. Most researchers seem to be preoccupied with the following question:
We sometimes get the uneasy feeling that we are doing it backwards. Computers were supposed to be tools, after all. Perhaps we should investigate another question instead:
The author is about to suggest a way to create programs that would use their experience of past executions in order to improve automatically their processor allocation. The proposed solution, while feasible (and hopefully elegant), will by no means be technologically simple. Please note that two different sets of runs of the same program, performed by two users, with possibly different data sets, may call for a different number of processors differently interconnected, in order to maximize speedup. How then can we know a priori the optimal computer architecture to run a given algorithm? We simply cannot. Indeed, such a fixed architecture may not exist.
We can, however, perform an adaptive search for optimal processor allocation independently at each user site. We will take our clues from nature.
Nature manages to evolve systems capable of ever-speedier computational feats. ('Evolve' is the term biologists would use; computer scientists usually prefer the term 'search'). For example, at some stage the early primates learned to throw stones in fights and hunts. If our survival depended on the acquired abilities to recognize and evade flying stones, then our skills of recognizing such airborne objects and forecasting their trajectories were only useful if we could execute the necessary algorithms before the obvious deadlines. The primates unable to meet the deadlines (of this and other nature) died prematurely. The search continues.
Biologists and psychologists frequently use the terms like 'evolution', 'brain', 'consciousness', 'dreams', etc. While their work has put us on the proper track in our efforts to maximize algorithm execution speed, these terms lack sufficiently precise meaning to be of direct use in computer science. For the purpose of this work, let us therefore define the following abstractions:
Brain: an ordered pair of two interconnected multiprocessor computers. The first computer is dedicated to run algorithms as needed by the user, while the second computer gathers the timing information and input data of the algorithm runs performed by the first computer. The second computer to fine-tune the architecture of the first computer will subsequently use this information. Obviously, when the first computer is subject to the reconfiguration, it cannot be available to the user. The second computer is never directly available to the user.
Alertness: the period of time when the first computer is available to its user. During this period the second computer gathers the timing information and the input data for the algorithms run by the first computer.
Sleep: the period of time when the architecture of the first computer is being reconfigured by the second computer, the first computer being unavailable to its user.
Dreams: acts of execution of user's algorithms for the purpose of obtaining timing information rather than providing user with the result. Such executions try out various processor configurations. The input data are identical to those used by the alert user.
Obviously, the above definitions, especially the one of the brain, would make most psychologists shudder. We will use them only as useful abstractions of more complex objects and ideas.
Our strategy will rely on our luck to live in an environment that is predictable to some extent. The changes that happen in it take place sufficiently slowly, so that we can manage to reconfigure our computer brains in order to maximize speedup (or, at least, to keep up with the environment). Let us take the weather for example. It turns out that the reliability of the simple forecast: The weather of tomorrow will be much like the weather of today is close to the best forecasting methods ever designed. In order to be able to come up with more reliable forecasts we perform our brain reconfigurations on the fly. The brains we use today were configured last night using the input data of yesterday. Luckily for us, this configuration is usually good enough for us to survive, and this night we will refine it, in order to keep up with the environment of tomorrow.
SEARCH FOR OPTIMAL COMPUTER ARCHITECTURE
As we have said, given the current state of computing technology, a brute force search for optimal processor allocation for most commercial algorithms would take longer than the age of the Universe. Let us justify this statement and suggest a more intelligent search strategy. First, let us clarify some terminology:
Algorithm: a finite sequence of instructions designed to provide a solution to the problem at hand within the required accuracy. When executed, it is required to reach the solution within a finite number of steps and is allowed to require only a finite amount of computational resources (time, memory, processors, etc.). Also called: a program.
Process: an act of single execution of an algorithm, with one input datum. In a given computer we may have a number of processes executing the same algorithm, typically with different input data (compilations, text editing sessions, device drivers, etc.).
Task: a single thread of execution. A process may consist of several cooperating tasks.
In other words, an algorithm a is a function:
a : D � R
operating from some set of input data D (also called domain of algorithm a) onto some set of results R (also called its range). We will also require that for at least one element d � D the algorithm a halts, i.e. its program produces some result r� R within finite number of steps. In short, we have required for the algorithm to be devoid of deadlock and livelock for at least one element d � D. Indeed, there may be a subset D of D for which the algorithm a halts. The trouble is that according to the halting problem theorem there is no algorithmic way to identify D within D.
Initially, we ensure experimentally that the algorithm a halts for at least one datum d � D, by writing, debugging and editing its program until it is forced to halt. A program may consist of several cooperating tasks. In current programming languages, each task is fired by a system call of the kind:
FORK (<task_id>, <startup_info>);
where <task_id> is typically a subprogram identifier, while <startup_info> contains auxiliary operating system instructions.
Consequently, it is possible to uniquely identify the tasks fired as the program executes. Let us consider the task T0 to be the main program. Then we start counting tasks being fired by counting the instances of execution of the FORK system call.
Consider a program executing the algorithm a with input datum d � D, consisting of n tasks T0, T1, T2,..., Tn-1. We will search for the optimal processor allocation, minimizing the execution time.
To say that we know that this program consists of n tasks, is to say that we have successfully executed it to a halt (perhaps on a uniprocessor, interleaving its tasks), using a particular input datum. In that case we could have noted not only its result r, but also its execution time tex. We will compare all possible processor allocations, considering tex as our deadline. Alternatively, we could have picked as the deadline any other value tdead, imposed on us by the environment (customer specification, benchmark requirement, etc.). In our search we will not be interested in processor allocations resulting in the execution time exceeding our deadline. Indeed, in such cases we will not bother to run our program to completion. We will just abort it when the deadline expires.
Obviously, the speed of execution depends on the hardware at our disposal. Suppose we have a computer with m processors P0, P1, P2,..., Pm-1. In general, these processors may have different characteristics (speed, word length, various amounts of on-chip memory, instruction set, etc.). We will keep allocating these processors to our tasks. The cooperation between tasks implies intertask synchronization and communication. In order not to sacrifice all the elegance of the advances in the machine independence afforded to us by software engineering we need to augment the FORK system call to:
FORK (<task_id>, <processor_id>, <startup_info>);
Using this new system call we will be able to explicitly assign a specified processor to a given task. Another system call will be needed to establish unbuffered, unidirectional logical links between two tasks that may run on two different processors:
LINK (<source_task_id>, <target_task_id>);
Obviously, when using the LINK system call we can create bi-directional links by using two unidirectional links of opposite orientation. Similarly, using the LINK primitive, with a little bit of programming effort, we can establish buffered links.
The bandwidth of these links will no doubt depend on the characteristics of the underlying hardware connection. In particular, the architecture of the computer at hand may not allow establishing a link between a particular pair of processors Px and Py. In this paper we will not treat this situation as a special case. We will rather assume that the established link has the bandwidth zero. Cooperating tasks using this particular link will not be able to complete so that the overall program meets the deadline tdead. In short, we assume that the execution of the LINK system call never fails.
Another reason for our program not meeting the deadline tdead might be the allocation of one of its tasks, say, Ti, to a processor Pk incapable of executing one of the instructions of code of Ti because the offending instruction is not in the processor's instruction set. We will assume then that the processor Pk hangs up, thus preventing the overall program to meet the deadline. We could, if we wanted to, prevent such a situation from happening, by scanning all the instructions forming the code of Ti and checking that they all are within the instruction set of Pk.
We will not follow this approach, however, because it is too strict. The code of the task Ti, apart from the offending instruction, may contain some conditional branch (i.e. IF) statements. There is no general way of knowing, which branch of the IF statement code (if any) the execution will follow, when our program is executed using the input datum d. Chances are, the section of code of Ti containing the offending statement may be bypassed entirely. For special cases this approach is not without merit, however.
In general, given the program with n tasks and the computer with m processors, there are a priori mn possible processor allocations. To illustrate this, consider all possible allocations of a two-task program on a computer of three processors. The possible allocations are listed in Table 1 below. The tasks are numbered 0 and 1, the processors are numbered 0 through 2.
Allocation Task 1 Task 2
#
0 0 0
1 0 1
2 0 2
3 1 0
4 1 1
5 1 2
6 2 0
7 2 1
8 2 2
Table 1. Possible allocations of a two-task program for a computer of three processors.
The first column of this table indicates the allocation number (0 through 8, 9 allocations in total; 9=32), the second and the third columns indicate the processor numbers allocated to task 1 and task 2 correspondingly.
The NP-completeness of the processor allocation problem is an obstacle. NP-complete problems are especially hard when attacked using uniprocessors. But most of them lend themselves to an easy treatment on parallel computers.
To illustrate this, consider the above example. Suppose that all three processors have different characteristics. If we had a computer with 27 processors, 9 of them of type 1, 9 of type 2, and 9 of type 3, we could try out all possible 9 allocations simultaneously. The whole allocation search experiment would last at most tdead time.
Granted, for nontrivial applications such a parallel search approach requires big multiprocessors. No wonder that our brains consist of more than 100 billion processors (neurons).
Fortunately, it will be rather infrequent that an application will require many processors of different types. Suppose that in the former example the processors 1 and 2 are identical. Suddenly, the number of possible allocations collapses dramatically. The allocations 1 and 2 become identical and it is enough to try out only one of them. Similarly, the allocations number 3 and 6 require testing of only one of them, and again the same goes for allocations 4, 5, 7 and 8. In total, we need to test four allocations instead of nine. The larger the application program, the larger the potential savings. Indeed, it would be ideal to utilize one type of processors only. As the studies of theory of computation indicate ([Davis and Weyuker, 1983], [Boolos and Jeffrey, 1987], [Epstein and Carnielli, 1989]), it turns out to be possible. It is no accident, therefore, that the human brain is made of processing elements of fundamentally one type (only neurons).
In our newly established terminology, the trial allocations are perceived as dreams. Indeed, one might suggest that the whole period of sleep consists of two subperiods: the first being the period of dreams, i.e. the search for optimal processor allocation, the other being the period of reconfiguration of the user computer, in order to reflect the identified optimal architecture.
These suggestions, although correct, are premature at this point. We have just run our program for one datum d. Another execution, for a different input value, may result in a different number of tasks being fired, and require a different optimal architecture.
It is hard, however, to resist the temptation to go a bit further and offer some tentative suggestions of implementation, at least for simple algorithms that use relatively few optimal architectures. We should avoid executing the LINK system calls at alert time on the user computer - their execution wastes time. Instead, we could prelink all the recognized optimal architectures for a given algorithm in the user computer and execute the algorithm on all of them simultaneously. As soon as the execution of one of these processes terminates, we offer the user the result and abort the processes running on different processor architectures.
To justify the correctness of these suggestions we must first establish a mechanism capable of recognizing potential parallelism in algorithms, and then propose a method for classifying emerging optimal architectures. Only then could we viably offer our suggestions for the implementation of computers with adaptive architectures.
AUTOMATIC RECOGNITION OF PARALLELISM IN ALGORITHMS
The concepts of algorithm and language are intertwined. An algorithm does not exist until it is written. Having written it down, we have implicitly chosen some language. Every language inhibits to some degree our capabilities of expression. We strive to design languages, which enforce as few such limitations as possible. It is hard, if not impossible, however, to design a high-level language in which all the algorithms, even those yet to be invented, are expressible. It looks therefore that the developments of linguistics and algorithms will proceed in parallel forever.
Neither an algorithm nor a language can exist without the existence of a computer. The converse is also true. The developments in computer technology, linguistics and algorithm design stimulate each other. In this paper we will not dwell on this fascinating subject.
The reason that we mentioned this subject at all is because we have recognized the need for languages capable of highlighting the inherent parallelism in algorithms. Not all expressions of the algorithm as an implementation of the function
a : D � R
are equivalent, in terms of the inherent possible parallelism. Indeed, an algorithm a could be considered a member of a larger set A of all possible expressions of the above function in all existing languages. It is the job of compilers to perform the necessary program transformations. We are interested in possible expressions that maximize the parallelism potential. Compilers also transform algorithms to fit the particular features of an underlying machine. Strictly speaking, machine independence is a fiction, albeit sometimes a very useful fiction.
The programming languages currently in use tend to suppress the evidence of parallelism in the algorithms they describe, therefore damaging the inherent structure of algorithms. A possible noble exception is OCCAM 2, a programming language in which it is possible to algorithmically undo such damages. Interested readers are directed to [Hoare, 1985], [INMOS, 1988], [Roscoe and Hoare, 1986], or, for a quick overview to [Burns, 1988]. Fortunately, the researchers in compiler technology start to recognize current linguistic deficiencies.
For the purpose of this paper we will assume now that we have at our disposal an implementation of the algorithm a with sufficient inherent parallelism. At the end of this section an algorithmic criterion for recognizing such parallel implementations will emerge.
Let us study the acts of execution of algorithms, with the intent of representing them as graphs. An executing algorithm, using some input datum, performs a number of operations, then halts. Let us represent these operations as nodes in our graphs. An operation may require some data as input, and may produce some results as output. For an operation requiring some input data we will draw arcs directed to the node representing that operation, the number of arcs being equal to the number of input data. Similarly, if an operation produces some result(s), we will draw arc(s) originating at the corresponding node and directed away from the node. If a given datum, required by some operation is produced by another operation, we will link the nodes representing the producer and consumer operations with an arc directed form the producer to the consumer node.
Note that in a graph so created, some arcs may not originate at any node. Similarly, there may be arcs pointing to no node at all. Such arcs will represent the program input and output data, correspondingly. We will call them the input and output arcs.
The graphs so constructed will be called algorithm graphs. Observe that the shape of the algorithm graph (number of nodes and their interconnecting arcs) may change if we execute the same algorithm for various data d � D from its domain. However, any algorithm is uniquely represented by the set of its algorithm graphs for those input data d � D, for which the algorithm halts.
Let us study the properties of the algorithm graphs rather than the algorithms themselves, with the intent of detecting a possible parallelism. Let us remove the input and output arcs, and observe the properties of the resulting directed, acyclic multigraphs.
By a critical path of a directed, acyclic graph we will mean the longest path (following arcs) contained in a graph. Such path need not be unique.
THEOREM 1. Any directed, acyclic graph with a finite number of nodes contains at least one node to which no arcs point and at least one node from which no arcs originate.
PROOF. This is obviously true for graphs containing no arcs. Suppose then that a graph contains at least one arc. Consider a starting node of any critical path in this graph. Suppose that there is an arc pointing to it. We may have two situations here:
- The node from which the arc originates belongs to the critical path. In that case we have found a circuit in our acyclic graph, contrary to our assumptions.
- The node from which the arc originates does not belong to the critical path. In that case we have found a path longer than the critical path, ending again in a contradiction.
Therefore, a starting node of any critical path in our graph is the node to which no arcs point. Similarly, it can be proven that the ending node of any critical path in our graph is the node from which no arcs originate.
Q.E.D.
This theorem permits us to arrange the nodes of our graph into three groups: the starting nodes, the internal nodes and the final nodes. If a critical path has a length of 2 or more, none of the three groups is empty. This node grouping amounts to the detection of a crude parallelism: all operations represented by the starting nodes could be executed in parallel, followed by similarly parallel execution of all operations represented as internal nodes, and terminating by the parallel execution of all operations depicted by the final nodes.
This finding may not be sufficient. We want to explore the entire parallelism that is hidden in our graph. Consider:
THEOREM 2. All nodes in an acyclic, directed graph of n nodes can be labeled with integers from {1, 2,..., s}, where s�n so that if an arc points from a node labeled with i to a node labeled with j then i<j.
PROOF. Consider all nodes to which no arcs point in the graph. Label them with 1 and remove them from the graph, together with arcs originating from these nodes. The resulting graph remains an acyclic, directed graph. Repeat the same exercise labeling all removed nodes with 2. Continue this procedure, until the whole graph is disassembled. The number of steps s this procedure is executed cannot exceed n, since each time we have removed at least one node.
Q.E.D.
The described labeling procedure of all nodes in our graph is called the strong topological sorting of a graph, or topological sorting, in short. This sorting permits us to detect the entire parallelism available in the graph. Obviously, all operations represented by nodes labeled with 1 can be executed as tasks in parallel, followed by all operations indicated by nodes labeled 2, etc. This is so because no nodes with identical labeling are connected with a producer/consumer arc.
For every graph we can identify the largest group of identically labeled nodes. Let us define the graph width to be equal to the number of nodes of that group. In the same vein, we can define the algorithm width as the maximum of the widths of all the graphs describing given algorithm.
Similarly, for every graph we can define its height as the length of the critical path plus one. By algorithm height we will understand the height of its tallest graph.
Earlier in this section we suggested an emergence of an algorithmic criterion for distinguishing between inferior and superior parallel implementations of algorithms. As we have said, each algorithm implementation corresponds to a family of algorithm graphs. Good parallel implementations will have a high algorithm width and a low algorithm height.
In future computer systems we would like to treat pools of processors as a fluid computational resource, much like we treat pages in paged virtual memory management systems now. Users should be free to dynamically draw processors from the pool and return them after use. The trouble with this approach (apart from the financial aspect) is that users have difficulty answering the following question:
The greedy answer: the number of processors in use will fluctuate during execution, we will need no more of them than the number of nodes in the algorithm graph. We will allocate them one per node.
However, if we assume that all processors execute their operations at equal speed, the number of processors needed drops considerably. With no loss of performance we can then settle for synchronous execution: all operations depicted by nodes labeled 1 should be executed initially, followed by all operations with labels 2, 3, etc. In this execution regime the number of processors needed equals algorithm width.
At this point of our analysis we may still worry that, in terms of the detected parallelism, we detected too much of it to handle. Certainly, keeping with modern programming strategies, we would like to exploit the parallelism in steps. We would like to analyze a conveniently small part of the available parallelism at any given time, deferring the analysis of the rest. To do that, we need a so-called weak topological sorting of our graph, defined by the following:
THEOREM 3. All nodes in an acyclic, directed graph of n nodes can be labeled with integers from {1, 2,..., s}, where s�n so that if an arc points from a node labeled with i to a node labeled with j then i�j.
PROOF. The proof is identical to the proof of theorem 2.
Q.E.D.
Such labeling of nodes in our graph allows us to organize the nodes into groups, but this time we are allowed to leave some sequential interdependencies between some operations belonging to the same group. This permits us to exploit the parallelism in an algorithm, perhaps at some procedure level, delaying the exploitation of parallelism in these procedures.
CLASSIFICATION OF OPTIMAL ARCHITECTURES
Given the algorithm a, the optimal processor allocation depends on the data d � D, for which its program is executed. The search for this allocation, while not brute force, must scan (at least partially) a vast number of configurations. This implies that the second computer of the brain, the one never directly available to the user, must be much larger than the first computer. This observation suggests the answer to the puzzle that perplexed the physiologists for some time. They wondered why the brain seems to violate the rules of the superbly efficient and parsimonious design of the human body. According to their estimates, we use approx. 5 to 10 per cent of our brain capacity. What is the remaining part for, and why did it not waste away if it is not in continuous use? The answer seems to be: it is in continuous use, but mainly at sleep time, searching for optimal processor allocations for a number of algorithms, and, for each algorithm, for many input data points.
For our algorithm a we do not need to know all optimal processor allocations for every datum d � D, but only for these values that the user encountered or is to encounter at alert time. Indeed, we have reasons to suspect that the distribution of probability of a given datum being encountered is not uniform over the set D.
We can think of the optimal computer architecture as a function f(d) of data points. Informally, the number of optimal configurations will be smaller than the number of data points. One could even argue that the number of elements in D is finite, although very large: every processor, having a finite word length, can represent only a finite number of different values. Sensors, providing input data from the environment can be considered processors. An alternate argument: we inhabit an environment that is of quantum nature, and our sensors have some ranges of operation. Therefore, we can perceive only a finite number of input data values. In this paper we will avoid the assumption of the finiteness of D. Instead, we will simply state:
THEOREM 4: The number of optimal configurations to be stored in our computer is finite.
PROOF. Having performed a finite number of runs for given input data values, we can come up with at most finite number of configurations, one for each run.
Q.E.D.
It is quite possible for two different data points x, y � D to obtain identical architectures f(x) = f(y). We say then that points x and y are equivalent. We expect to see regions in D such that all input data from each region call for the same multiprocessor architecture. We could run some pattern recognition programs to identify these regions. After some experience has been gathered, we might try to guess the region to which new and untested data points belong. This exercise could be performed both at sleep time and at alert time. Our current successes with computer systems equipped with the virtual memory management mechanisms provide sufficient motivation to try out this idea.
To formalize this approach, let us consider a relation of equivalence E over the set D. For x, y � D we will write xEy if and only if f(x) = f(y). Relations of equivalence have the following properties:
(i) ("x � D) xEx
(ii) ("x, y � D) if xEy then yEx
(iii) ("x, y, z � D) if xEy and yEz then xEz
These properties are known respectively as the reflexive, symmetric and transitive laws of any equivalence relation.
Let us further define:
Quotient map: Let E be an equivalence relation in D. Let further P(D) be a powerset of D, i.e. the set of all subsets of D. The quotient map associated with E is the function:
j : D � P(D) with values defined by j(x) = {y | xEy}
The quotient map is also called natural map. The various sets j(x) are called equivalence classes of E. The set of all equivalence classes, i.e. the range of j, is called the quotient set of D by E. A member of an equivalence class is often called the representative of the class.
Finally, let us define:
Partition: a partition P of the set D is a collection of nonempty subsets of D such that for each
d � D there is exactly one B� P with d � B.
In other words, P is an exhaustive collection of mutually exclusive subsets of D.
Our cognitive exercise of learning the properties of the partition of D that would reflect the optimal processor architectures is based on the following theorem, well known to the mathematicians specializing in abstract analysis, which we will give here without proof:
THEOREM 5. Let E be an equivalence relation in D, and let Q be the quotient set of D by E. Then Q is a partition of D. Conversely, if P is any partition of D, then there is a unique equivalence relation F in D having P as its quotient set.
Readers interested in the details of the proof might peruse [Gleason, 1991], or any other book on abstract analysis.
IMPLEMENTATION CONSIDERATIONS
The requirements for computational speed are most stringent for real time systems, biological or otherwise. In these systems, obtaining results within deadlines is of paramount importance. Since it is always possible to formulate a deadline impossible to meet, we will therefore consider only 'practical' deadlines, i.e. deadlines for which feasible multiprocessor architectures, given the current state of hardware technology, exist.
The fastest way of implementing an algorithm is to store the results of computation in a table, indexed by the argument values. The table should be created at sleep time and accessed in parallel at alert time. This is how the mathematicians define a function: as a particular set of ordered pairs. The pairs could be stored perhaps in parallel access registers (PARs, also known in the study of operating Systems as page address registers). If this maximally parallel approach does not enable us to meet the deadline, no other software approach will. The only hope left is in the performance improvements of hardware technology.
Unfortunately, due to substantial cost and memory limitations this method is feasible only for algorithms with very small domains or for selected argument values. The utilization of PARs in virtual memory management systems could be an example of its successful application.
The next best thing is to store all optimal architectures for the algorithm and use them in parallel to obtain the result. As soon as it is obtained on one of the architectures, the processes running on other architectures are aborted.
This approach is guaranteed to work (assuming 'practical' deadlines) only for simple algorithms, where it is easy to identify the proper partitioning of the algorithm's domain, and where the number of the equivalence classes is sufficiently small so that we can simultaneously store all the optimal architectures, one for each equivalence class.
What if we cannot meet these storage requirements? This situation can arise for nontrivial algorithms. It almost certainly arises in the case of the human brain, which runs a vast number of nontrivial algorithms.
Suppose we are to run a nontrivial algorithm for the first time. We have no idea how many processor architectures might be called for, and what is the optimal one for the current datum. We can run the algorithm on a uniprocessor. This will probably make us miss the deadline, but at least we will be able to recognize and remember the algorithm graph. If we have a multiprocessor with a vast number of randomly connected processors, it will not hurt to initiate simultaneously the execution of this algorithm in a number of places in the network, hoping that some local processor configuration will luckily math the desired algorithm graph. Each such process we will delegate the emerging parallel operations to other processors along the existing hardware links. This does not guarantee success, but the larger the network and the denser the interconnection mesh, the more such processes we can fire, and the higher therefore is the probability that one of these processes will not hang up, and perhaps even meet the deadline. In any case, we do not expect spectacular performance during the first alert period.
During the first period of sleep, we will fine-tune the processor allocations by identifying architectures for the newly recognized algorithm graphs. The best allocation would assign a separate processor to each operation represented by the node in the graph. For small multiprocessors this may not be practical, in terms of the number of processors needed. A good allocation does not serialize operations that could be executed in parallel. In terms of topologically sorted algorithm graphs, a single processor allocation is a subset of nodes in the graph such that every node has a different label. The operations represented by nodes listed in an allocation are not intended to be executed in parallel. The architecture is the set of allocations such that each graph node is listed in one allocation only, and no nodes are omitted. If the processors available were at a premium, the architecture of interest would contain the smallest number of allocations.
Unfortunately, the algorithm graphs detect only the inherent parallelism between operations, but contain no information concerning the time needed to execute various operations. This is why we have dreams... A compromise is needed between the most parsimonious architecture (in terms of the number of processors used) and the fastest. The compromise architecture is the most parsimonious among those which permit us to meet the deadline.
As time passes and the sleep and alert periods alternate, we continue to enrich our library of selected architectures. The real time performance of our algorithm improves, but we may approach the limits of storage capacity, in terms of the number of stored architectures. We may be interested in reducing the number of architectures by giving up those, which have not been in use for a long time. This is typically done in the assumption that the environment changed, so that these architectures are of lesser value now. We certainly observe the reduction of non-refreshed skills in humans.
Earlier in this section we have recognized the benefits of including in the user computer the largest possible network of processors with the biggest number of interconnections, technology permitting. These benefits obviously apply to the second computer of the brain as well. As an added bonus, our artificial brain can attain the seemingly miraculous capability of self-repair: in some cases it will be possible to reconstruct lost information regarding the identified optimal processor architectures.
In the long run, in a relatively stable environment, the user part of the brain will be required to run a relatively unchanging mix of algorithms, and the architecture optimization searches will yield diminishing returns. The user part of the brain will become very efficient but highly specialized: it will be able to execute certain functions only, much like a real-time controller in an industrial setting. We could say that it loses its intelligence.
A subsequent change in the environment will require running new algorithms, for which our biological real-time controller might be ill suited. Instead of abandoning it and starting the search for a better controller, evolution prefers to leave it alone doing what it is good at, and to divide the remaining part of the brain into two regions: the first, accessible to the user, and the second, optimizing the performance of the first region.
The anatomy of the brain reflects this progress of evolution through punctuated equilibria [Eldredge, Gould, 1972]. At the first glance we can easily identify three different regions: the brainstem, the cerebellum and the cerebrum. The brainstem, the smallest of the three, is responsible for controlling the most ancient body functions like breathing and digestion. The larger cerebellum is controlling more recent but still routine functions, like maintaining posture and controlling body movements. The largest of the three regions, the cerebrum, consisting of two hemispheres linked by the corpus callosum, is the site of our conscious and intelligent activities [Sagan, 1977].
Coming back to the realm of computer science, let us paraphrase our definition of the brain: it is a large network of vastly interconnected multiprocessors. One part of the network is allocated to run user algorithms, while the other part optimizes the performance of the first part. The demarcation line, defining where the user part of the brain ends and the optimizing part begins, has always been left completely arbitrary. As the overall size of the network grows, the demarcation line might move and the newly defined brain would start optimizing certain new algorithms, perhaps including some of the old optimization routines.
The evolution continues.
REFERENCES