PFractal by Philip Nelson

Download

Introduction

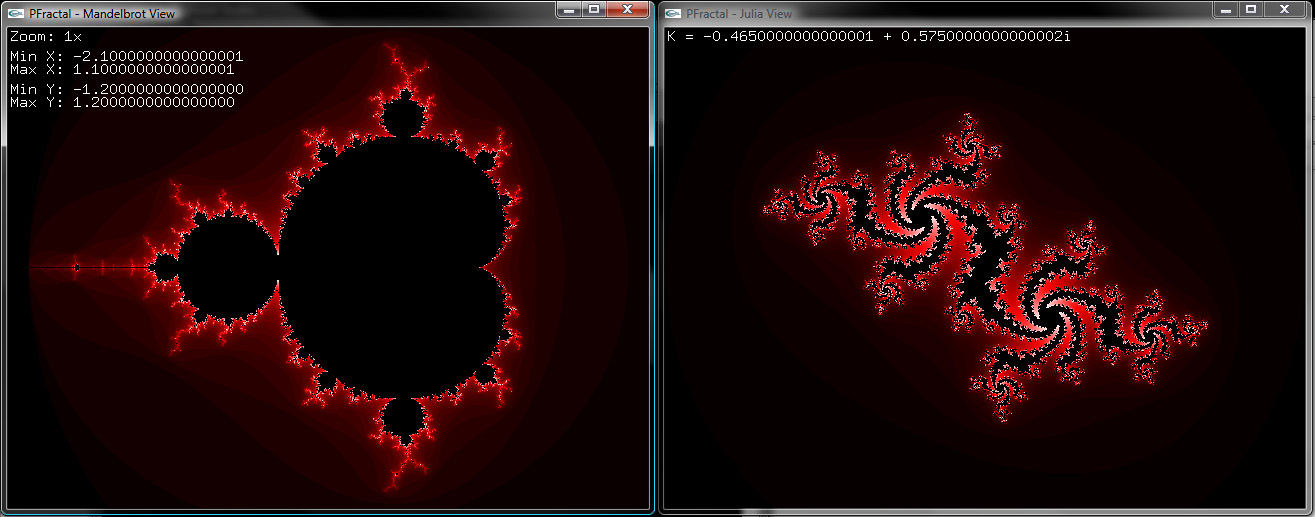
PFractal is an interactive environment to view and explore the Mandelbrot and Julia fractal sets. Here is a screenshot of PFractal.

Mandelbrot Set

The Mandelbrot set is the set of complex numbers c that are not infinite when n approaches infinity where,
z₀ = c
z_{n + 1} = z_n² + c

Julia Set

A Julia set is a set of complex numbers c that is not infinite when n approaches infinity where,
z₀ = c
z_{n + 1} = z_n² + K

The z_n function differs from the Mandelbrot set because K is a constant complex number. This means that for each complex number, there exists a Julia set.

Design and Functionality

The design and functionality of PFractal goes hand-in-hand. This is because of the actual simplicity of the functions that produce these spectacular fractal images.

When PFractal is first loaded, it displays the full Mandelbrot set. On the Julia View, it displays the Julia set for the complex number K = 0 + 0i. The colors are initialized to the Black -> Red -> White gradient. The details of the gradient will be discussed later.

Every pixel on the screen is mapped to a complex number. Initially, the Mandelbrot set is displayed from -2.1 to 1.1 on the x (real) axis, and from -1.2 to 1.2 on the y (imaginary) axis. As the user zooms in on the Mandelbrot set, the minimum and maximum real and imaginary coordinates are reduced by the selected factor. Every Julia set is displayed from -2 to 2 on the x (real) axis, and from -1.5 to 1.5 on the y (imaginary) axis. These minimum and maximum coordinates of the complex plane being displayed are used to map any given coordinate on the Cartesian plane to a complex number. For both the Mandelbrot and the Julia sets, every pixel is converted to a complex number that will represent the c value and be tested whether or not it belongs to the set. As the user's mouse moves in the Mandelbrot window, the coordinate of the mouse is converted to a complex number that will represent the constant K in the Julia set, and is drawn in the Julia window at real time.

Since the Mandelbrot and Julia sets are contained within a radius of 2 around the origin of the complex plane, we can easily determine if a point does not belong to the set by checking if sqrt(a² + b²) > 2, where z = a + bi. This simplifies to checking if a² + b² > 4.

Since z is a complex number that begins equal to c, calculating z_{n + 1} = z_n² + c is not that difficult. Following the complex number arithmetic rules,
    z_{n + 1} = (a + bi)² + c
    z_{n + 1} = (a + bi)(a + bi) + c
    z_{n + 1} = a² + abi + abi + (bi)² + c
    z_{n + 1} = a² - b² + 2abi + c
Since a² - b² + 2abi is a complex number, the real portion is a² - b² and the imaginary portion is 2ab. To add the second complex number c, simply add the real portion of c to a² - b² and the imaginary portion of c to 2ab.

This computes z_{n + 1} = z_n² + c. For the Mandelbrot set, z_{n + 1} is computed a maximum of 50 * Zoom times when Zoom is positive, or just 50 times if Zoom is negative. For the Julia set, z_{n + 1} is computed a maximum of 30 times. This allows for the Julia set to be updated real time relative to the mouse position.

The set of points belonging to the Mandelbrot and Julia sets are colored black. In addition, six preset gradients have been set up:

Black -> Red -> White

Black -> Green -> White

Black -> Blue -> White

Black -> Yellow -> White

Black -> Cyan -> White

Black -> Purple -> White

These colors are applied with respect to the number of iterations it took to find that a complex point c was not in the set. In the case of the first gradient, Black -> Red -> White, if c is found to not be in the set within the first half of the maximum number of iterations, the color would gradually go from black to red. If c is found to not be in the set within the second half of the maximum number of iterations, the color would gradually go from red to white. The modulo operator makes this very easy. Applying colors to the Mandelbrot and Julia sets show the borders of the sets much clearer.

User Guide

Moving the mouse with the screen focus on the Mandelbrot View will display the corresponding Julia set for the mouse position on the complex plane.

Right-clicking on the Mandelbrot View will bring up a menu with the following options:

Set Color Scheme - This sets the gradient that will be used for coloring the Mandelbrot and Julia sets.

Black -> Red -> White

Black -> Green -> White

Black -> Blue -> White

Black -> Yellow -> White

Black -> Cyan -> White

Black -> Purple -> White

Set Zoom Factor - This sets the factor that the zoom action will take when clicking on the Mandelbrot set.

Zoom In 16x

Zoom In 8x

Zoom In 4x

Zoom In 2x

Disable Zoom

Zoom Out 2x

Zoom Out 4x

Zoom Out 8x

Zoom Out 16x

Reset - This resets the Mandelbrot and Julia views to the original state.
Save Mandelbrot - This will save the Mandelbrot view to a .png file.
Save Julia - This will save the Julia view to a .png file.
Exit - This will exit the program.

Explore and be creative!

References

I used a variety of web sites for information and inspiration.

Back to COSC 4P98 Projects